引言

大家好啊，我是前端拿破轮😋。

只要你做过字符串类的算法题目，或者学习过数据结构与算法的课程，那么对于KMP算法一定不陌生。不少同学对此恨之入骨，总是看了当时觉得会了，隔一段时间就又做不出来了。对此有网友生动地给其取名为K(看)M(毛)P(片)算法😂😂😂。可见大部分同学对它真是爱之深，恨之切啊。

今天拿破轮就带大家深入分析KMP算法，彻底搞明白，以后爸妈再也不用担心我的KMP算法了🤩🤩🤩。

温馨提示：万字长文，点赞收藏转发后阅读效果更佳😏😏😏。

老规则，带着问题读文章，阅读完本文后，如果能够完整准确地回答这些问题，那么对KMP算法就掌握的应该就差不多了。

  1. 什么是KMP算法？
  2. 为什么需要KMP算法，用来解决什么问题？
  3. 如何使用KMP算法？
  4. 使用KMP算法有哪些注意的事项？

1. 什么是KMP算法？

KMP三个字母并没有什么特殊的含义，就是取了提出该方法的三个作者名字的首字母而已。

该论文原名FAST PATTERN MATCHING IN STRINGS，翻译为中文就是在字符串中进行快速的模式匹配。论文作者有三人，分别是Donald E. Knuth、James H. Morris Jr.以及Vaughan R. Pratt，于1997年发表在刊物SIAM Journal on Computing上。

我们首先来分析一下这篇论文的题目，字符串很好理解，不再赘述。那什么是模式呢？什么又是模式匹配呢？

在计算机科学中，尤其是在字符串算法中，“模式”（Pattern）指的是你要查找的那段子字符串，也叫 模板 或 匹配串。

举个例子：

  • 主串(Text): "ababcabcacbab"
  • 模式串(Pattern): "abcac"
  • 目标: 找到主串中是否存在"abcac"这个子串，是否出现过，如果出现过就返回出现的位置。

到这里我们已经很清楚了，所谓KMP算法，就是找到主串中子串的出现位置。

注意：主串也叫文本串，子串也叫模式串，是相同含义的不同称呼。

2. 为什么需要KMP算法，用来解决什么问题？

KMP算法解决的是模式匹配的问题，但是模式匹配还有很多中解决方案，并不止KMP一种。

那模式匹配在实际中有什么应用呢？

其实是非常多的：

  • 文本搜索：当我们在vscode,word或者网页等等地方按下Ctrl + F进行搜索时，不就是一个模式匹配问题吗？需要在整个文本中匹配我们的目标子串。
  • 正则表达式匹配
  • DNA序列比对
  • 编辑器代码高亮

等等，模式匹配的需求可以说非常常见。

本文我们就具体化为最简单的问题，就是编写一个函数，传入文本串和模式串，返回在文本串中模式串出现的第一个下标，如果文本串中没有模式串，则返回-1。

对应leetcode28-找出字符串中第一个匹配的下标

在本文中，拿破轮将以TypeScript语言为例进行分析和代码编写。其他语言同理，语言知识实现工具，掌握算法的核心思想才是最重要的。

3. 如何使用KMP算法？

3.1 暴力方法怎么解决？

在说KMP算法前，我们先来自己思考一下如何解决这个题目？

其实暴力解法并不难想到，只需要两层for循环来遍历主串，外层for循环的位置作为目标子串的开始位置，内层for循环逐个对比主串与目标子串的字符。

一旦某个字符不匹配，就跳出内层循环，移动开始位置，进入下一次外层循环。

如果在某次内层循环遍历结束后，所有的字符都匹配，那么就返回此时的起始位置作为结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
function strStr(haystack: string, needle: string): number {
  // 剪枝：如果主串长度比模式串小，直接返回-1
  if (haystack.length < needle.length) return -1;

  // 外层循环，遍历开始位置
  for (let i = 0; i <= haystack.length - needle.length; i++) {
    // 设置一个标志变量，用来指示本轮循环是否匹配
    let isMatched: boolean = true;

    // 内层循环，依次对比每一个字符串
    for (let j = 0; j < needle.length; j++) {
      // 如果不匹配，则将标志变量设置为false，并跳出内层循环
      if (haystack[i + j] !== needle[j]) {
        isMatched = false;
        break;
      }
    }

    // 根据标志变量来判断是正常遍历完本次内层循环，还是不匹配跳出
    if (isMatched) {
      // 如果是正常退出，直接返回本次外层循环的下标，即开始值，作为结果
      return i;
    }
    // 如果不是正常退出，接着进行下一个外层循环，不用进行操作
  }
  // 当外层循环全部遍历结束都没有返回正确的开始位置，说明不匹配，返回-1
  return -1;
};

动画如下图所示：

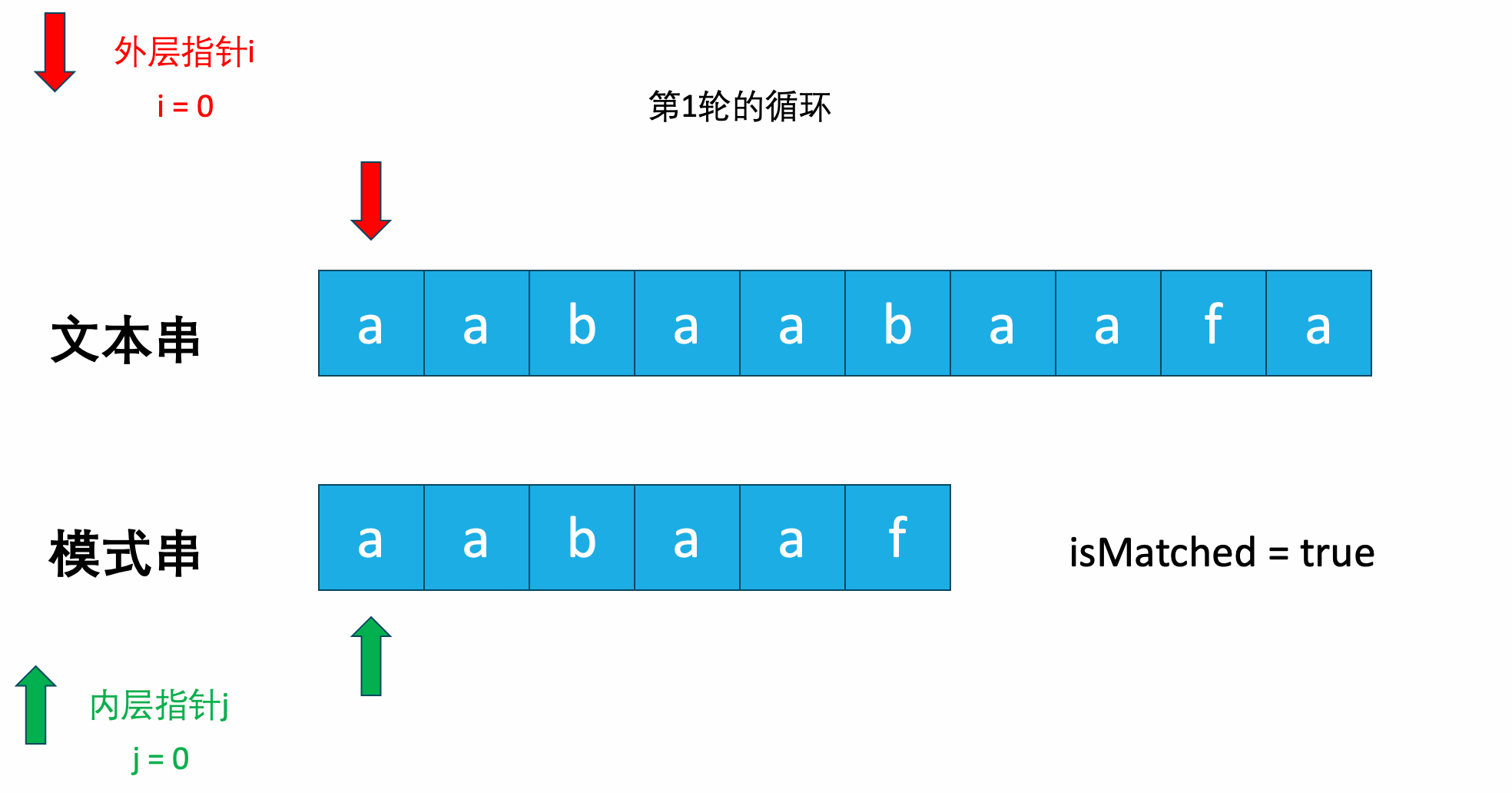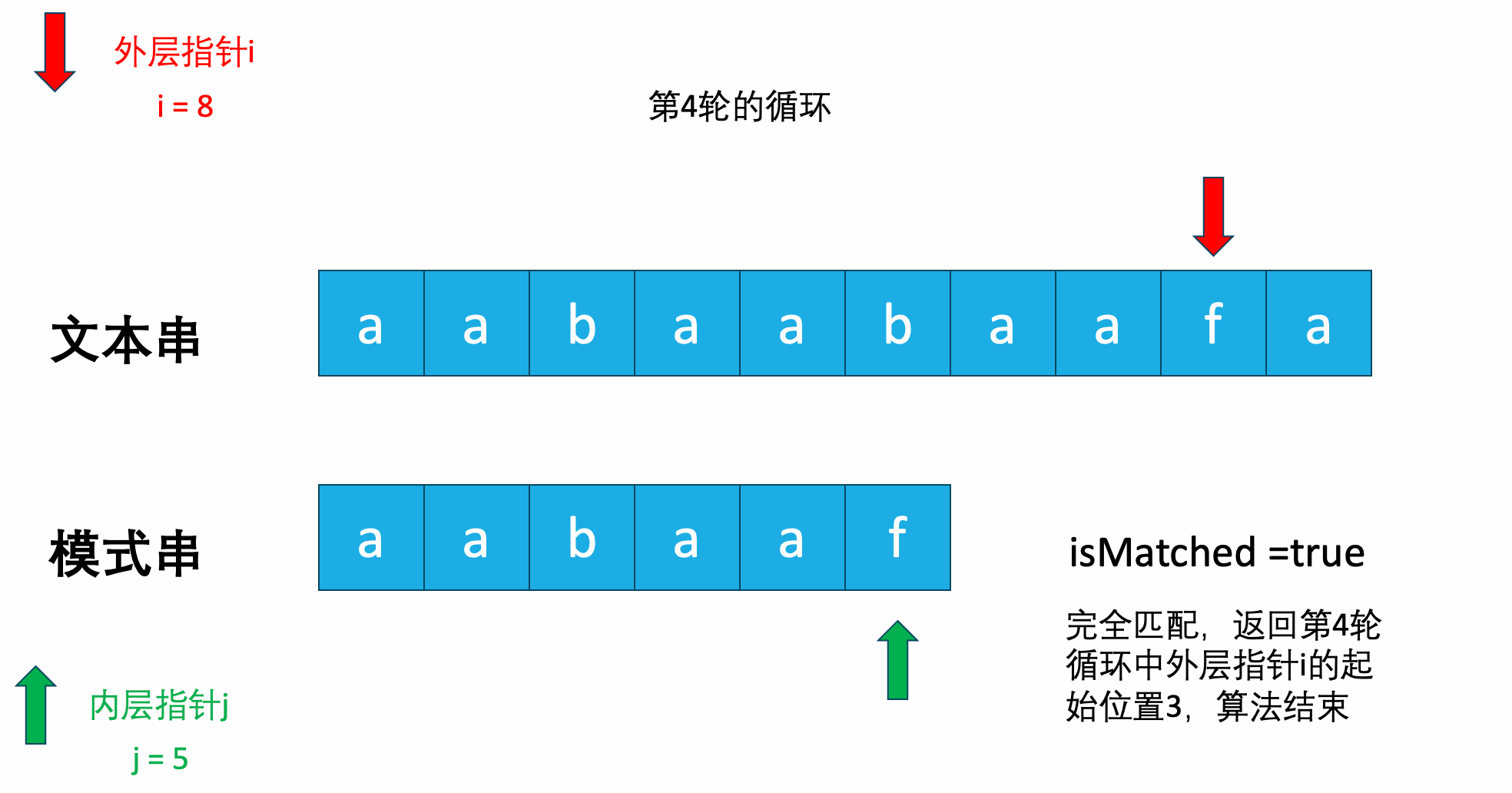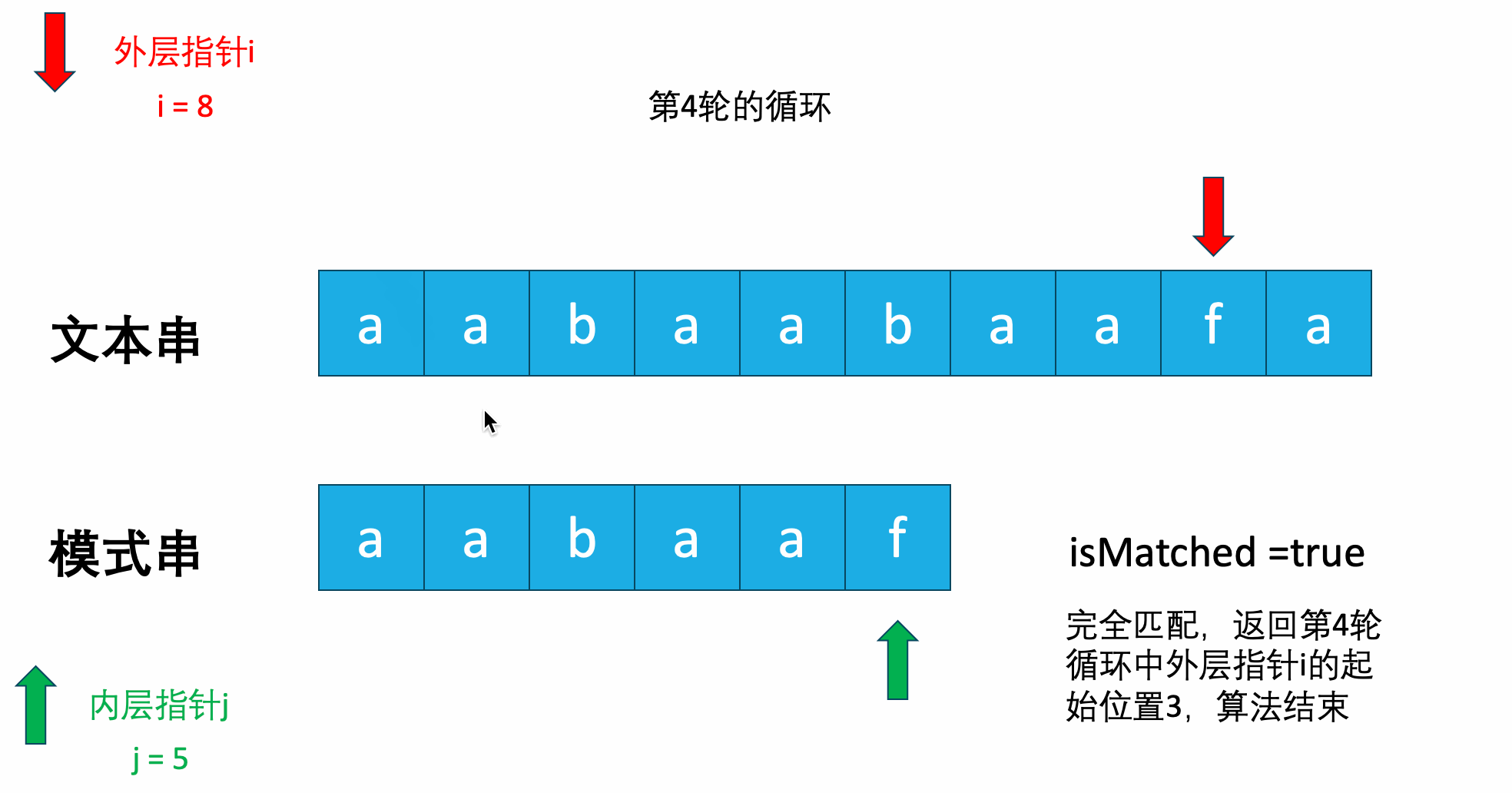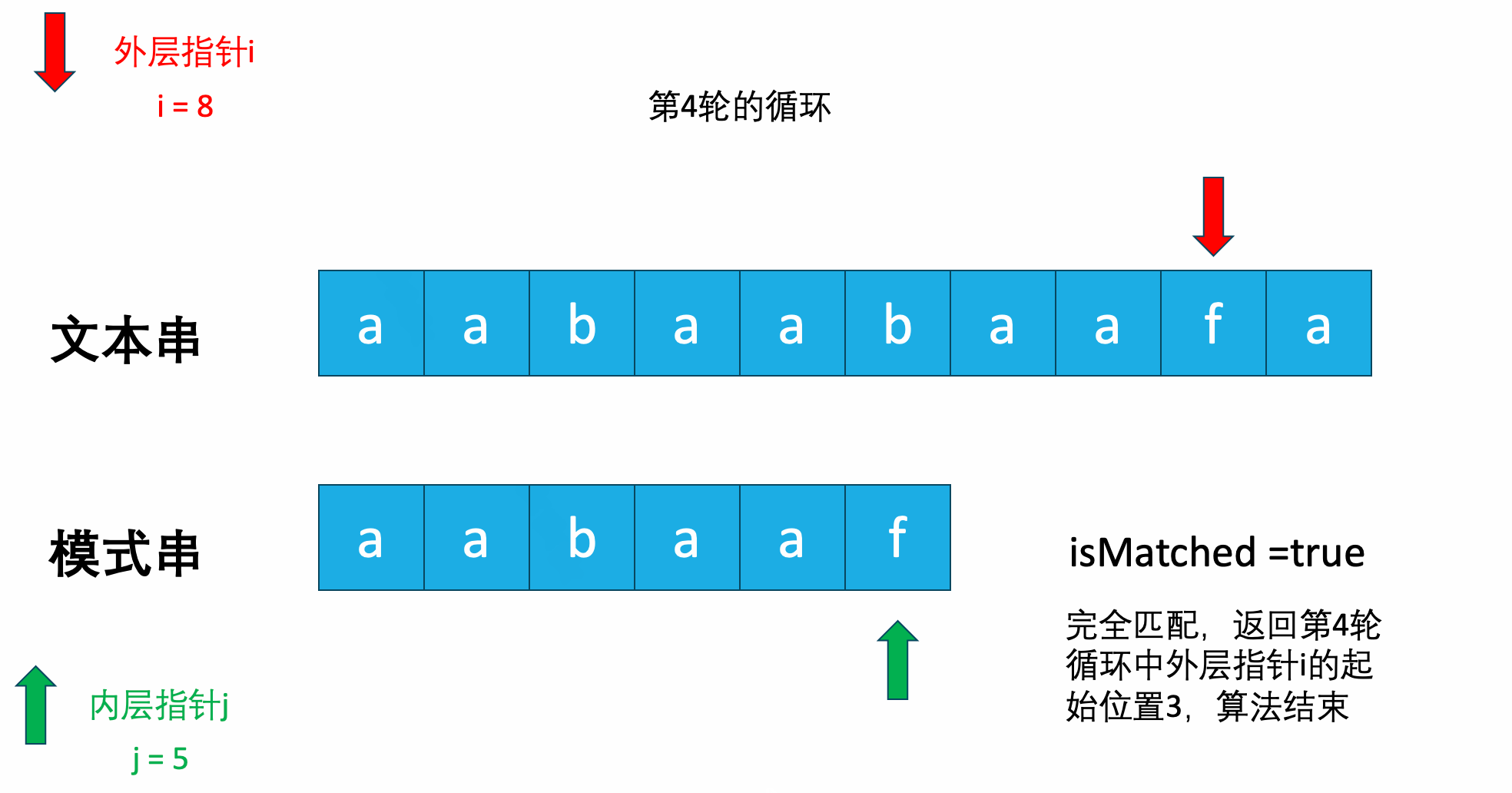
PixPin_2025-07-12_17-13-00

上述解法也可以成功AC在leetcode上的题目，但是时间复杂度过高。由于有两层for循环，所以最坏的时间复杂度达到了$O(N*M)$，其中的N和M分别是主串和模式串的长度。虽然空间复杂度是常数级别的，因为只使用了两个指针，但是空间复杂度的缺陷导致了当问题规模大到一定程度后，时间实在太久。这就是KMP算法要解决的问题。

有没有什么办法可以在$O(N)$的时间复杂度内解决此类问题呢？

其实仔细观察刚才的动画就可以发现，好像有一些轮次的循环，我们在循环之前就知道，这一轮肯定匹配不上了。

比如这里：

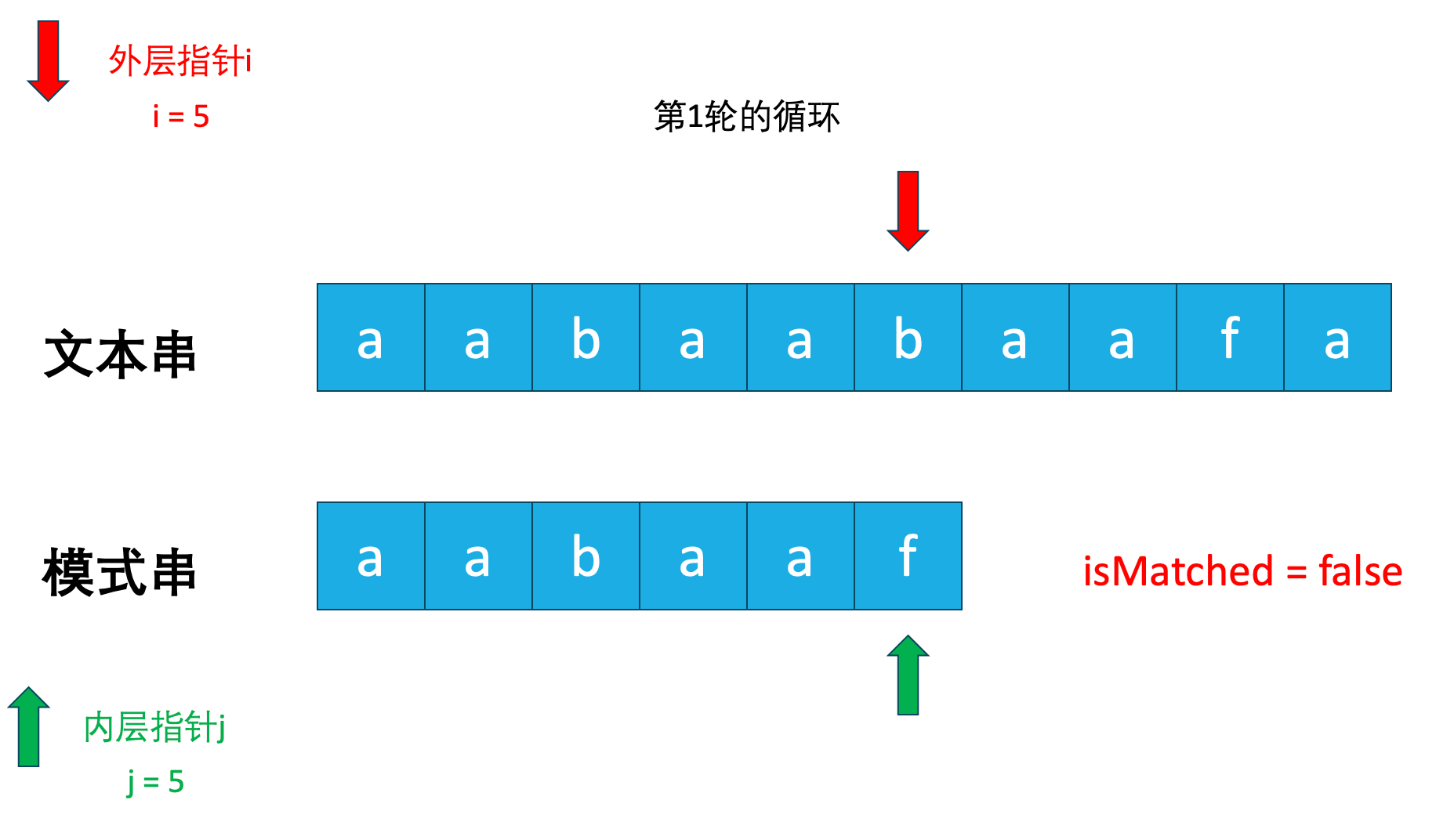
20250712171907

在第1轮循环中，我们在最后一个字母发现是不匹配的，按照暴力算法的解法，此时i会移动到文本串下标为1的位置，而j会重新移动到模式串下标为0的位置。开始第2轮的匹配，就像下图一样。

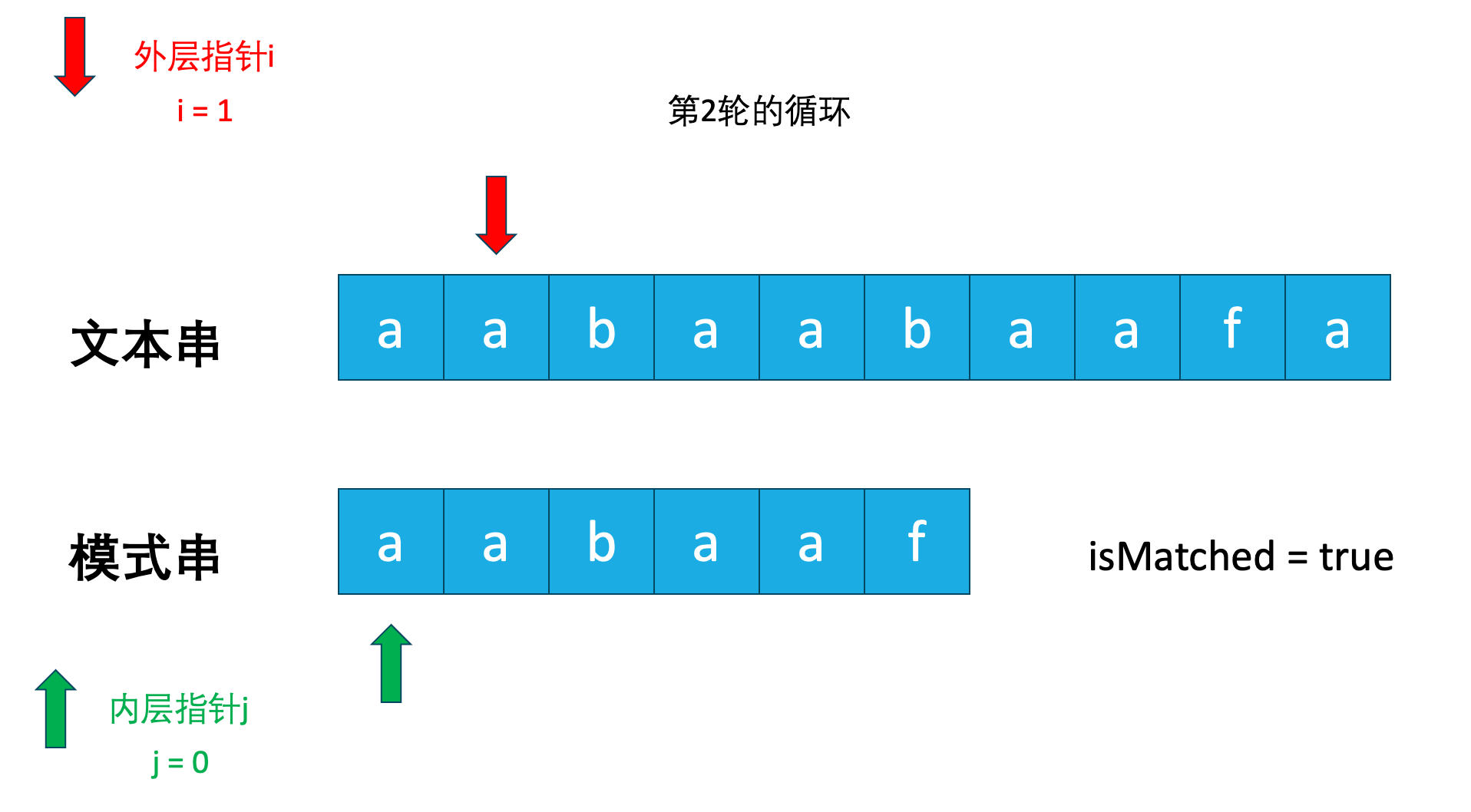
20250712172542

每一轮循环我们都需要从头开始遍历模式串，那么有没有一种方法可以让我们不要从头开始遍历呢？

为了找到当前不匹配后下一个应该从哪里匹配。KMP算法提出了Next数组的概念。