引言

大家好啊，我是前端拿破轮😁。

跟着卡哥学算法有一段时间了，通过代码随想录的学习，受益匪浅，首先向卡哥致敬🫡。

但是在学习过程中我也发现了一些问题，很多当时理解了并且AC的题目过一段时间就又忘记了，或者不能完美的写出来。根据费曼学习法，光有输入的知识掌握的是不够牢靠的，所以我决定按照代码随想录的顺序，输出自己的刷题总结和思考。同时，由于以前学习过程使用的是JavaScript,而在2025年的今天，TypeScript几乎成了必备项，所以本专题内容也将使用TypeScript，来巩固自己的TypeScript语言能力。

题目信息

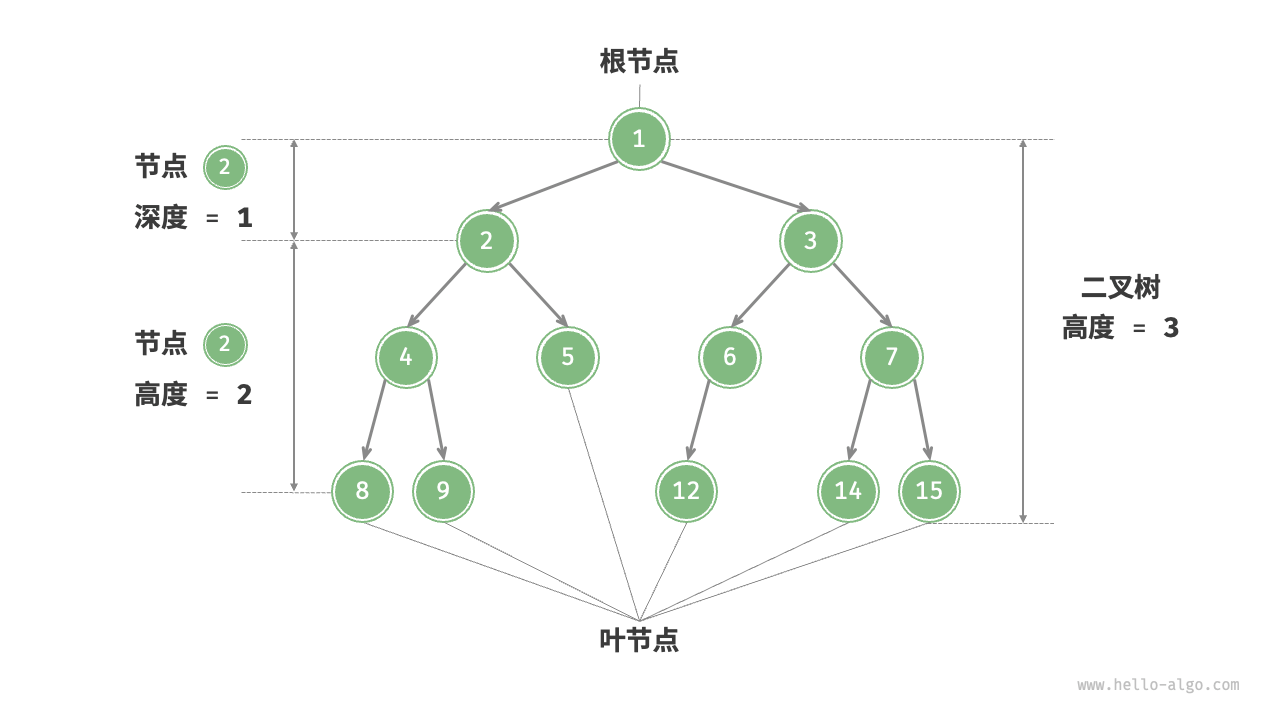
二叉树的最大深度

leetcode题目链接

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

题目分析

求解这道题目，有多种方式，可以使用DFS的递归方式求解，也可以使用BFS层序遍历来求解。

递归方式

还是按照递归三部曲

  1. 确定递归函数的参数和返回值以及他们的意义

我们来看下题目提供的函数能否满足条件

1
2
3
function maxDepth(root: TreeNode | null): number {
    
};

这个函数的参数是一个根节点，返回值是一个数字，表示这个数的最大深度。那么这个是否可以直接作为我们的递归函数呢？我们还是来分析原始问题和子问题的性质是否相同，左右子树的最大深度和整棵树的最大深度有没有关系呢？答案是肯定的，整棵树的的最大深度不就是左右子树最大深度的最大值中较大的那一个再+1吗？+1加的是根节点自身的高度。

所以题目的函数是可以直接用作递归函数的。

  1. 确定终止条件

当前根节点为null时终止，返回0即可。

  1. 确定单层递归逻辑

用技巧，我们只考虑最外层的递归，就是根节点那里。所以首先对左右子树分别求最大深度，然后求出两者之间较大的那一个，然后+1返回即可。

层序遍历方式

层序遍历要利用队列来进行。首先初始化最大深度为0，然后按照正常的层序遍历方式，在每一层遍历开始时，将最大深度+1，不用进行实际的的遍历节点存储，，因为我们并不需要返回遍历结果。遍历结束后，返回最大深度即可。

题解

递归方式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function maxDepth(root: TreeNode | null): number {
  // 终止条件
  if (!root) return 0;

  // 单层递归逻辑
  return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
}

时间复杂度：$O(n)$

空间复杂度：$O(h)$, h是树的高度

层序遍历方式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
function maxDepth(root: TreeNode | null): number {
  // 边界剪枝
  if (!root) return 0;

  // 辅助队列
  const queue: TreeNode[] = [];

  // 根节点入队
  queue.push(root);

  // 最大深度
  let maxDepth = 0;

  // 当队列非空时，开始遍历
  while (queue.length) {
    // 最大深度+1
    maxDepth++;

    // 记录当前层节点数
    const len = queue.length;

    // 遍历当前层
    for (let i = 0; i < len; i++) {
      // 出队元素
      const node = queue.shift();

      // 左子节点入队
      node.left && queue.push(node.left);

      // 右子节点入队
      node.right && queue.push(node.right);
    }
  }
  return maxDepth;
}

时间复杂度：$O(n)$

空间复杂度：$O(n)$

总结

对于二叉树的最大深度，难度相对来说较低。用DFS和BFS都可以解决。没有什么容易出错的地方。但是下一篇要讲的二叉树的最小深度就有容易出错的地方了。感兴趣的同学可以订阅本专栏，持续更新。

好了，这篇文章就到这里啦，如果对您有所帮助，欢迎点赞,收藏,分享👍👍👍。您的认可是我更新的最大动力。由于笔者水平有限，难免有疏漏不足之处，欢迎各位大佬评论区指正。

往期推荐✨✨✨

我是前端拿破轮，关注我，一起学习前端知识，我们下期见！